Numeros Complejos 2

Números Complejos 2

Demostración de la formula de Euler

Hemos demostrado que un número complejo se puede poner de tres formas distintas

z₁=(a,b)=a+bi=r(cos(Arg z)+isen(Arg z)

La primera es un par ordenado, la segunda es la forma binómica y la tercera polar o trigonométrica, vamos a calcular una cuarta forma, llamada exponencial.

Para ello necesitamos utilizar el número e, un número irracional.

La mejor definición de e es que ln e = 1

El logaritmo neperiano de se puede definir como:

ln x= ∫ (1) a (x) de (1/x)dx

Demostración:

Lo que queremos demostrar es que z=re^{iArg z}

Vamos a usar funciones:

f(x)= e^ix

g(x)=cos(x)+isen(x)

Queremos demostrar que son iguales:

Se puede hacer por Series de Taylor o por aplicaciones de derivadas. Usare aplicaciones de derivadas para demostrarlo:

Primero se pone una condicion inicial:

f(0)=1

g(0)=1+0=1

Ambas valen 1 en x=0, esto no es suficiente, solo tenemos que son iguales en un punto.

Derivemos ambas funciones:

f’(x)=e^ix *x

g’(x)=-sen(x)+icos(x)

No son iguales por ahora, pero el menos del seno se puede poner como i², por lo tanto:

g’(x)=i²sen(x)+icos(x)=i(cos x+isenx)

Si nos fijamos

g(x)=cos(x)+isen(x) así que g’(x)=i*g(x)

y además

f(x)=e^ix; f’(x)= e^ix*i=f(x)*i

Por lo tanto tenemos que

g’(x)=i*g(x)

f’(x)=i*f(x)

Es la misma ecuación diferencial, la derivada de una funcion da ella misma por I

Y encima tienen la misma condicion inicial, en x=0 su valor es 1.

Por lo tanto son iguales:

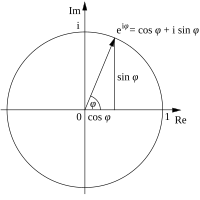
f(x)=g(x); e^ix=cos(x)+isen(x)

z=(a,b)=a+bi=r(cos(Arg z)+ isen(Arg z)=e^{iArg z}

Y si sustituimos por π

e^iπ=cos π + isen π=-1+0=-1

Por lo tanto e^iπ=-1 ( Identidad de Euler)