Introduccion a los Numeros Complejos
Si intentas resolver esta ecuación, obtendras que x2=-1;
esto quiere decir que un número al cuadrado da resultado a un número
negativo. Esto no es posible en el campo de los números reales ya
que ningún numero elevado a un exponente par da como resultado un
número negativo.
Y para empezar hay que definir que es un número complejo
Un número complejo es un par ordenado de numeros reales (a,b) siendo
a y b dos números cualesquiera. Al número complejo se le suele
denominar z. Pongamos un ejemplo
z=(3,-2) ; a suele denominarse como la parte real (3) y b como la
parte imaginaria (-2)
Operacion suma de numeros
z1=(a,b)=(-3,2)
z2=(c,d)=(2,1)
z1+z2=(a+c,b+d)=(-3+2,2+1)=(-1,3)
Multiplicación de complejos
z1*z2=(ac-bd,ad+bc)=(-3*2-2*1,-3*1+2*2)=(-8,1)
Vamos a poner un ejemplo, para obtener una forma más facil de poner
los números complejos:
(a,0)+(x,0)=(a+x,0)
(a+0)*(x,0)=(ax-0,0+0)=(ax,0)
Si se fija, al poner segunda componente 0, la suma se comporta
exactamente igual que con los numeros reales, y la multiplicación.
Por lo tanto (a,0)=a, porque solo tiene componente real.
Definamos entonces como (0,1)=i
ya que:
yi=(y,0)*(0,1)=(0-0,y+0)
yi=(0,y)
Tomemos un número complejo
(a,b)=(a,0)+(0,b)=a+bi ( Nueva
nomenclatura )
Por lo tanto, los complejos se
pueden escribir por ahora con dos formas.
z=(a+b)=a+bi
Ahora hagamos un comentario:
i2=i*i=(0,1)*(0,1)=(0-1,0+0)=(-1,0);
Usando la definición anterior: i2=-1
De aqui se define esto como que I
es la raiz cuadrada de -1.
(a+bi)*(c+di)=ac+adi+bci+bdi2=ac-bd+i(ad+bc)
( Propiedad distributiva)
Notaciones polar o trigonómetrica
de un complejo
El
argumento de un complejo, es en el plano complejo, el ángulo que
forma el complejo desde el origen. Arg z= x+2π
n
siendo n un numero entero.
Usando
coordenadas polares
Definimos
el sen (Arg z)= b/r y cos (Arg z)= a/r siendo r la distancia del
origen al punto que forma el complejo, esto es trigonómetria básica.
Por
lo tanto
a=r
cos (Arg z)
b=r
sen(Arg z)
Y
usando teorema de Pitagoras: r=(a2+b2)1/2
Con
estas definiciones, si sustituimos:
bi=risen(Arg
z)
z=(a,b)=a+bi=(rcos(Arg
z) + risen(Arg z))=r(cos(Arg z ) + isen(Arg z))
Por
lo tanto tenemos tres métodos por ahora de nombrar un complejo, el
último lo hare en la siguiente entrada de números complejos.


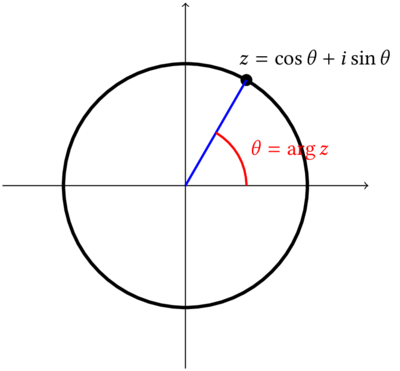
Comentarios
Publicar un comentario